Resummation about the separatrix

Resummation is a powerful tool that lets us take approximate expressions and rewrite in such a way that they are more faithful to the true solution. My paper explores using a resummation of strong-field self-force results to resum the post-Minkowskian expressions for the scattering angle.

First of all, what is the post-Minkowksian expansion? In this approximation, you expand the spacetime around flat space (the Minkowski metric) which in practice means expanding the spacetime in powers of Newton’s constant. Trajectories in flat space are straight lines, so the post-Minkowskian expansion naturally describes deviations from straight lines, i.e. weak-field scattering with a small deflection angle.

The self-force expansion is a different expansion we can do where we assume one black hole is much bigger than the other and then expand around the spacetime of the larger black hole. The is expansion is equally valid at any separation as long as the ratio between the masses of the two black holes is sufficiently small.

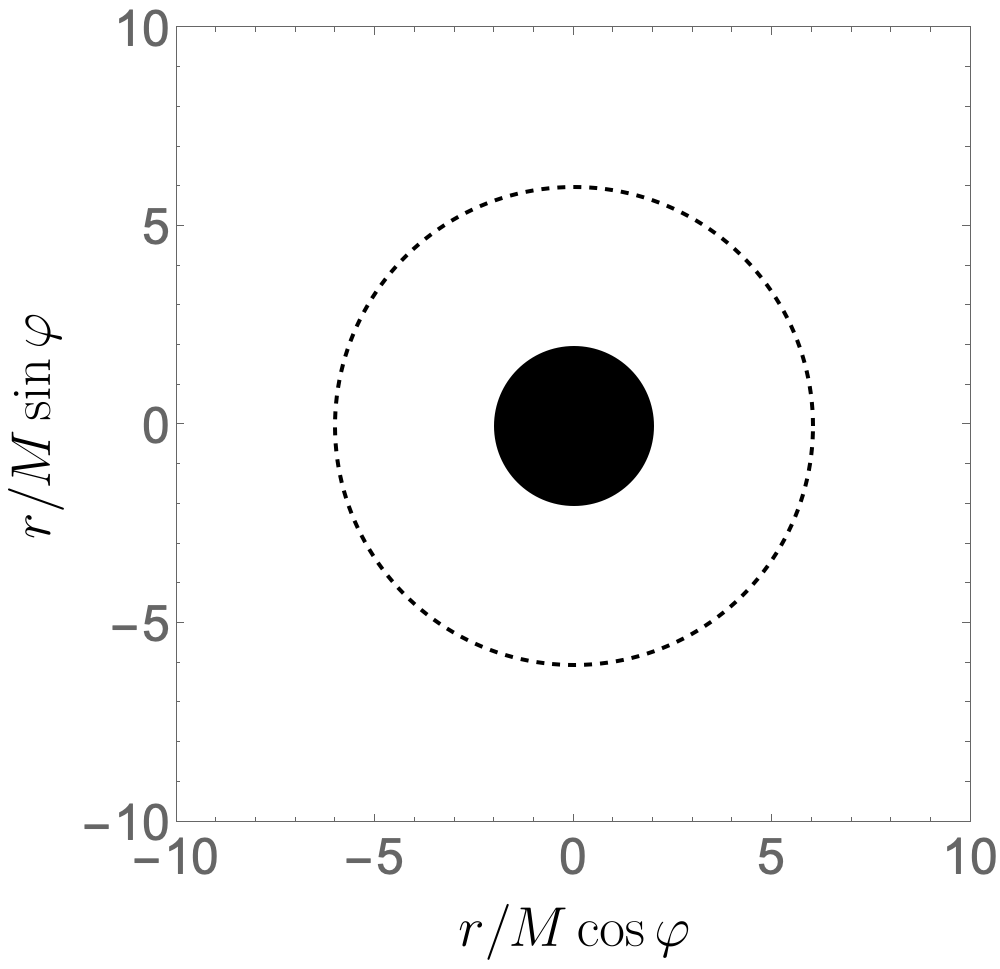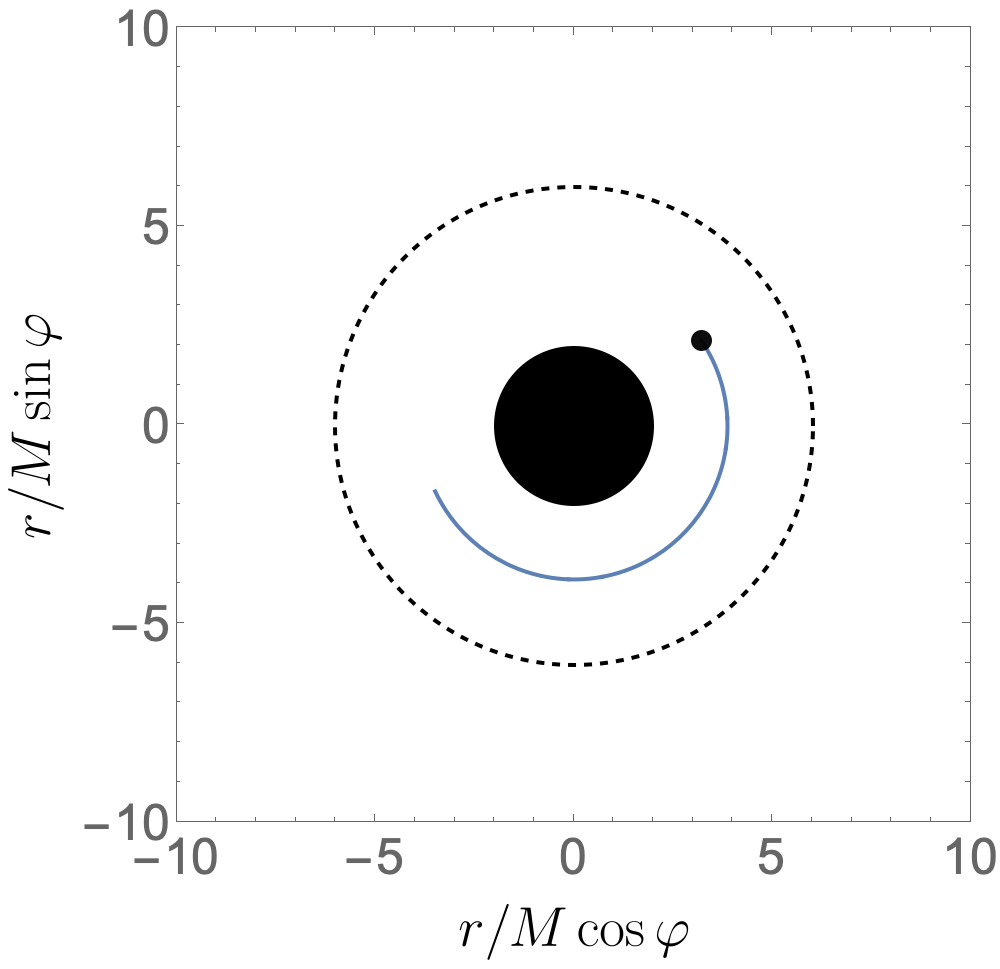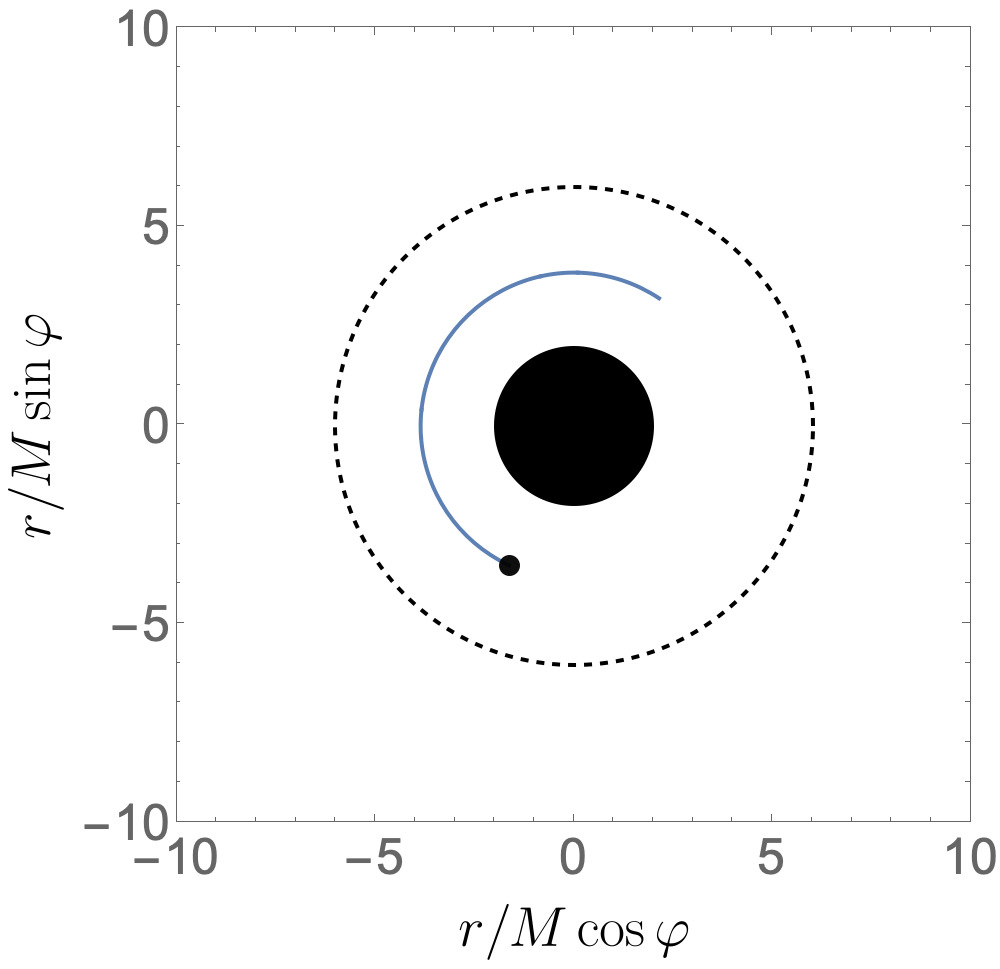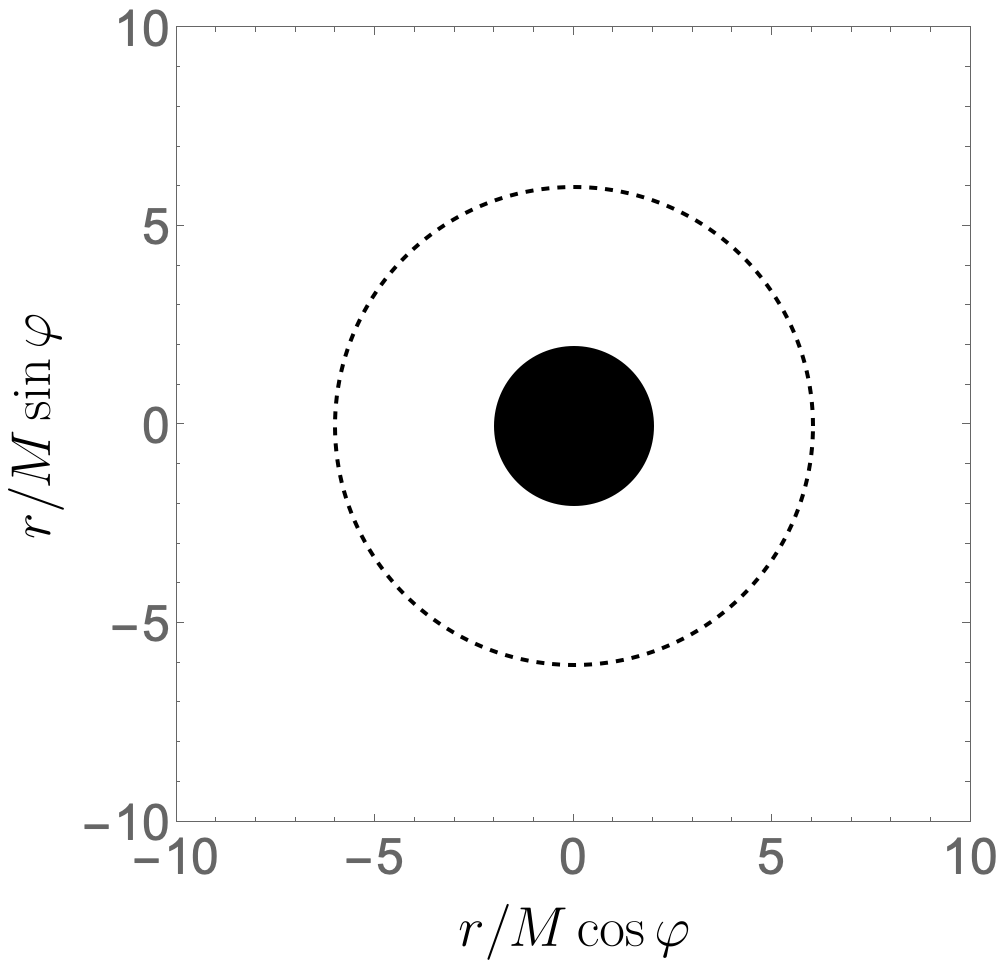
Trajectories of unbound binary black hole systems
Figure 1: A strong-field geodesic orbit of a test particle around a non-spinning black hole. The dashed circle shows the location of the innermost stable circular orbit (ISCO) for reference.

What this project does is use information from self-force to resum the post-Minkowskian expansion so that it is valid all the way into the strong field. The way we do this is by utilising the fact that when in the strong field, a small object can do many near-circular orbits around the large black hole, as shown in Figure 1. By adding the number of revolutions we do in the strong field (from self-force) to the weak field post-Minkowskian expansion we gain a result more faithful to the true answer.

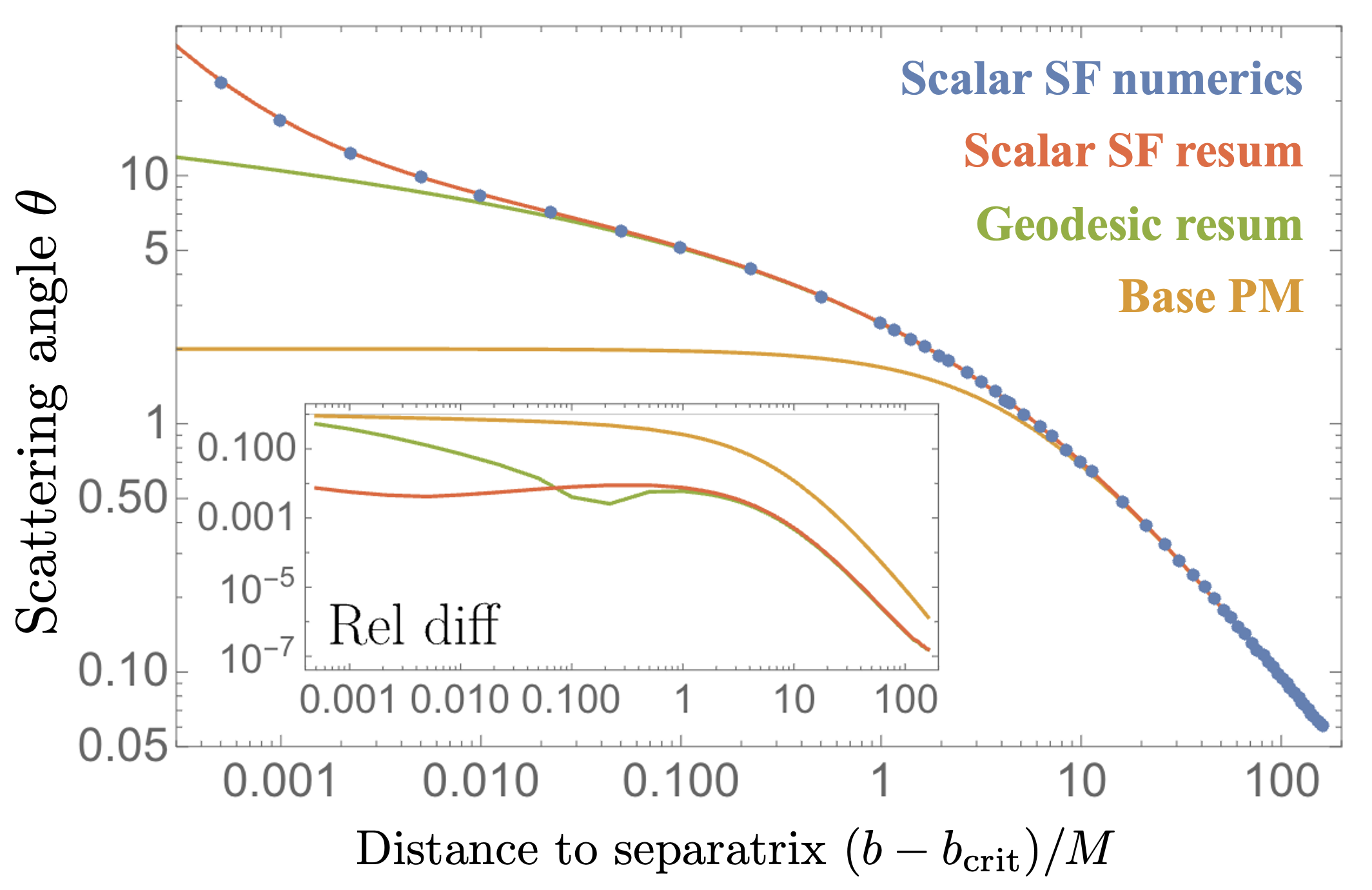
Figure 2 shows this for the test case of a scalar charge orbiting a black hole. The blue dots show the “exact” numerics and the lines show different post-Minkowksian models. The base post-Minkowksian model (orange) agrees with large separations (to the right of the plot), but starts to disagree as we get more into the strong field. By using the self-force information to build a resummed model (red) we can see that this improves the agreement to the numerics keeping it below 1% across the whole parameter space!

This proof of principle calculations shows how a simple addtion of information from the strong-field can be used to improve weak-field analytic models across the whole parameter space.

Scattering angle results for anti-aligned spin and unequal-mass systems
Figure 2: A modified version of Figure 8 from the paper showing scattering angle results for a scalar charge toy model. The blue dots show the exact numerical results and the different coloured lines show different post-Minkowskian models. The inset shows the relative difference of each model to the numerical results.