Introduction to self-force theory

Extreme mass-ratio inspirals (EMRIs) are black hole binaries in which a compact object of mass $m$ (a stellar-mass black hole or neutron star) orbits and slowly spirals into a supermassive black hole of mass $M \gg m$. Figure 1 shows that as the small body orbits the larger black hole, it emits a long, intricate gravitational wave signal lasting months to years, which will be detected by the forthcoming LISA mission. EMRIs will trace out millions of waveform cycles in band, allowing LISA to measure black-hole properties and strong-field gravity with exquisite precision.
To model these signals we use gravitational self-force (SF) theory, which treats the small body as a perturbation of the background black hole spacetime. Quantities are expanded in the small mass-ratio of the system $\varepsilon = m/M \ll 1$. For example, the spacetime metric is written as
\[g_{\mu\nu} = g^{(0)}_{\mu\nu} + \varepsilon\, h^{(1)}_{\mu\nu} + \varepsilon^{2} h^{(2)}_{\mu\nu} + \ldots,\]where $g^{(0)}$ is the background (Schwarzschild/Kerr) metric of the big black hole and $h^{(n)}$ are the $n$-th-order perturbations generated by the small body. The corresponding SF corrects the geodesic motion of a test body causing a slow inspiral. In a more intuitive way, the small body warps spacetime, then “feels” the field it created, slightly altering its own path.
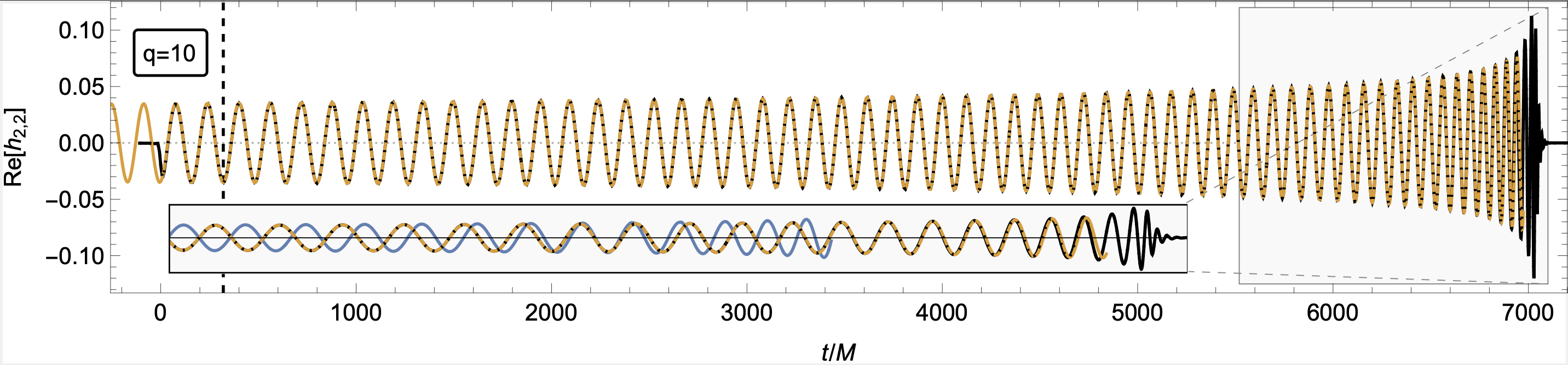
The SF calculations need to stay accurate over all $\sim10^5-10^6$ cycles where it can be detected by LISA. In order to do this we need information from second-order SF (2SF), i.e the $\varepsilon^{2}$ above, to remain accurate across the entire inspiral. The current state-of-the-art calculations have produced 2SF waveforms for a particle on a quasicircular orbit inpsiraling into a Schwarzschild black hole. Figure 2 shows a comparison of the SF waveform against numerical relativity for a mass ratio of $\varepsilon=10$. The two waveforms show good agreement up until near merger when the SF expansion breaks down.